Wochentagsformel
Gaußsche Wochentagsformel zum Berechnen eines Wochentages an einem bestimmten Datum. Wochentage hier online berechnen, Wochentags-Formel als Android-App downloaden, oder Erläuterung der Formel betrachten.
Sie möchten wissen, welcher Wochentag ein bestimmtes Datum war, beziehungsweise sein wird?
Kein Problem!
Mit der Gaußschen Wochentagsformel können Sie den Tag ganz einfach berechnen.
Jetzt neu: Android™-App
Android™-App kostenlos für Ihr Mobiltelefon herunterladen:
Hinweis:
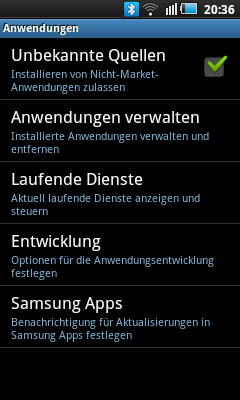
Damit Sie die Applikation installieren können, müssen Sie in den Einstellungen unter Anwendungen die Option "Unbekannte Quellen - Installieren von Nicht-Market-Anwendungen zulassen" aktivieren und bei nach der Installation gegebenfalls wieder deaktivieren.
Information:
Mit der Gaußschen Wochentagsformel kann man den Wochentag eines bestimmten Datums berechnen. Wie der Name schon sagt, wurde die Formel von dem Mathematiker Carl Friedrich Gauß entwickelt. Die Formel basiert auf den Gregorianischen Kalender. Somit gilt diese Formel seit dem 15. Oktober 1582 und ist gültig bis zur nächsten Kalenderreform. Die Wochentagsformel wird auch häufig in der Informatik eingesetzt.
Die Formel:
| Variable | Bedeutung |
|---|---|
| A | Hilfsgröße A |
| m | Monat |
| d | Tag |
| y | die letzten zwei Ziffern der Jahreszahl |
| c | die ersten zwei Ziffern der Jahreszahl |
A = ⌊2,6 ∗ m - 0.2⌋ + d + y + ⌊y/4⌋ + ⌊c/4⌋ − 2 ∗ c
Information:
⌊..........Gaußklammer (das heißt, dass darin stehende Werte abzurunden sind)
| Variable m | Monat |
|---|---|
| März | 1 |
| April | 2 |
| Mai | 3 |
| Juni | 4 |
| Juli | 5 |
| August | 6 |
| September | 7 |
| Oktober | 8 |
| November | 9 |
| Dezember | 10 |
| Jänner | 11 |
| Februar | 12 |
R = A mod 7
Information: Modulo
Modulo bezeichnet eine mathematische Funktion, welche den Divisionsrest zweier Zahlen bestimmt. Man kann Modulo auch als Divisionsalgorithmus bezeichnen.
| Modulo von Hilfsgröße A (Kennzahl R) | Wochentag |
|---|---|
| 0 | Sonntag |
| 1 | Montag |
| 2 | Dienstag |
| 3 | Mittwoch |
| 4 | Donnerstag |
| 5 | Freitag |
| 6 | Samstag |
Information: Ausnahmen
Die Gaußsche Wochentagsformel berücksichtigt zum Beispiel auch Schaltjahre. Das macht sie so komplex. Leider fehlen auch keine Ausnahmen. Ein kleiner Trost: es sind nur zwei. ;-)
1. Ausnahme: Bei den Monaten Jänner und Februar ist von der Jahreszahl 1 zu subtrahieren.
2. Ausnahme: Wenn die Hilfsgröße kleiner als 0 ist, muss man zur Hilfsgröße A 7 addieren.
Berechnung für 2. April 2025:
Monat = April ⇒ m = 2
d = 2
y = 25
c = 20
A = ⌊2,6 ∗ 2 − 0,2⌋ + 2 + 25 + ⌊25/4⌋ + ⌊20/4⌋ − 2 ∗ 20
A = ⌊5,2 − 0,2⌋ + 27 + ⌊6,25⌋ + ⌊5⌋ − 40
A = ⌊5⌋ + 27 + ⌊6,25⌋ + ⌊5⌋ − 40
A = 5 + 27 + 6 + 5 − 40
A = 10
R = A mod 7
R = 3 = (7 ∗ 1 + 3) = 10 ⇒ 3 Rest.
3 Rest ⇒ Mittwoch

